Nástroje
Ekonomický kalendář
Otevírací hodiny trhu
Úrokové sazby
Kalendář svátků
Forexový trh
Forex volatilita
Korelace Forexu
Novinky na Forexu
Analýza forexu
COT údaje
Likvidita
Forex kalkulačky
Forex Tepelná mapa
Ekonomické ukazatele
Komunita
Komunita
Systémy
Nejpopulárnější systémy
Strategie
Soutěže
Forexové grafy
Forexový sentiment
Indikátor Outlook
Recenze
Brokeři
Proprietární obchodní firmy
Služby VPS
Poskytovatelé signálu
Služby programování EA
Partnerské programy
Služby PAMM Brokera
Služby slevového programu
Obchodní platformy
Odborní poradci
Kryptoburzy
Kurzy obchodování
& copy; 2025 Myfxbook Ltd. Všechna práva vyhrazena.
UPOZORNĚNÍ NA VYSOKÉ RIZIKO: Obchodování s devizami přináší vysokou úroveň rizika, které nemusí být vhodné pro všechny investory.
Páka vytváří další rizika a ztráty. Než se rozhodnete obchodovat s devizami, důkladně zvažte své investiční cíle, úroveň zkušeností a toleranci vůči riziku.
Můžete přijít o část nebo všechny své počáteční investice. Neinvestujte peníze, které si nemůžete dovolit ztratit. Educate yourself on the risks associated with foreign exchange trading, and seek advice from an independent financial or tax advisor if you have any questions.
Všechny údaje a informace jsou poskytovány "tak, jak jsou". pouze pro informační účely a nejsou určeny pro obchodní účely nebo rady.
Výkonnost v minulosti neznamená výkonnost v budoucnosti.
You have an Ad Blocker!
Myfxbook is a site supported by advertisements. Here are two ways for you to continue browsing:
Ad Free Subscription
nebo
Disable your Ad Blocker
Already subscribed?
Přihlásit se
Nejste přihlášeni
Tato funkce je k dispozici pouze registrovaným uživatelům.
Registrace je bezplatná a trvá méně než minutu.
Pokračujte kliknutím na tlačítko "Registrovat".
Pokud již jste členem a využíváte naše služby, stačí se přihlásit.
Registrace je bezplatná a trvá méně než minutu.
Pokračujte kliknutím na tlačítko "Registrovat".
Pokud již jste členem a využíváte naše služby, stačí se přihlásit.
Unblock Notifications
You've blocked browser notifications for Myfxbook.com. Please enable it:
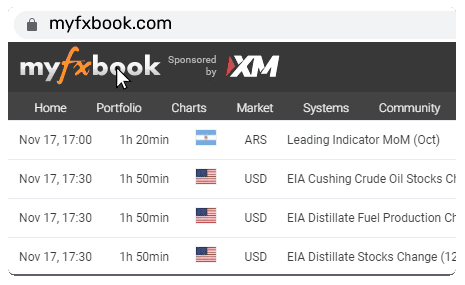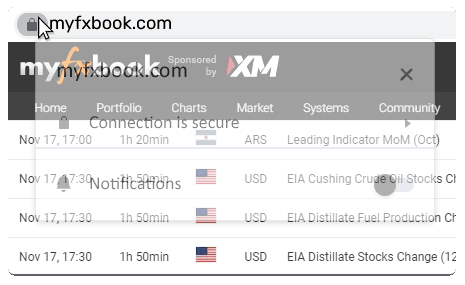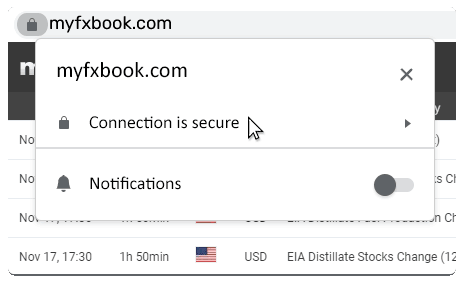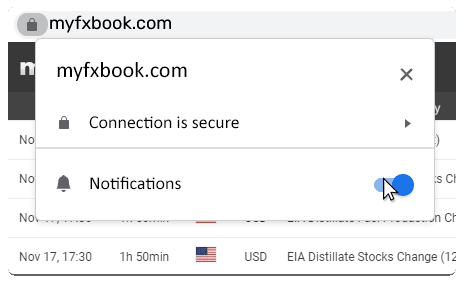

You can disable notifications at any time from your browser.









