Kalkulator Fibonacciego
What are Fibonacci retracement levels?
Fibonacci retracement levels are support and resistance levels that are calculated using several important points in a price series such as a high and a low. It is based on the famous Fibonacci sequence invented by the Italian mathematician Leonardo Pisano Bigollo. [1] A fibonacci number is an integer in an infinite mathematical sequence (1,1,2,3,5…) starting from the number 1 and then followed by the sum of the previous 2 integers.
How to use Fibonacci in Forex trading?
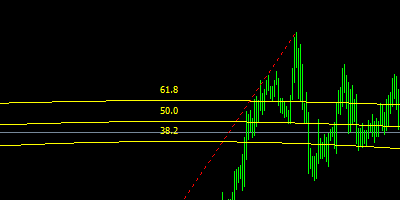
Fibonacci trading levels are often used as important support or resistance levels (or turning points) of a price. This is because numbers in the sequence are frequently found in nature, which many traders believe in their relevance in the financial markets as well.. In trading, the Fibonacci levels are represented by the following retracement levels: 23.6%, 38.2%, 61.8%, 78.6%, 161.8%, 261.8% (a 50% retracement levels and 100% are also often used although they are not official fibonacci levels).
For example a EURUSD price of 1.3200 can retrace by 23.6% to 1.0084 which can be used as a support to buy at. Consequently, these levels can be also used as a stop loss or take profit levels.
Does Fibonacci work in trading?
Fibonacci is another tool in your trading which can be applied to price action alongside other indicators and technical analysis techniques (such as moving averages). They can help you build your trading plan and have an easy-to-follow trading style since they can be mathematically calculated without any human discretion (unlike news trading for example).
Are the Fibonacci Retracements useful in day trading?
Fibonacci retracement tool can be used in any timeframe and any trading style whether it is short term trading (scalping) or long term (trend following). It is considered to be more meaningful in longer timeframes (ie 30 minutes and above) to reduce short term market noise.
How to use Fibonacci retracement?
Since Fibonacci can be applied to any mathematical sequence, it can be used in many different formats with your trading, for example :
Fibonacci Extension (Retracements) - as the name suggests, horizontal extensions are drawn on a price chart using the Fibonacci level to predict the target price levels.
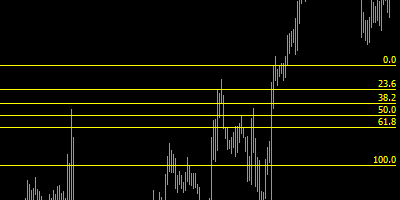
Fibonacci Fan - same as extensions, only the targets are plotted using trendlines, originating in the same price point.
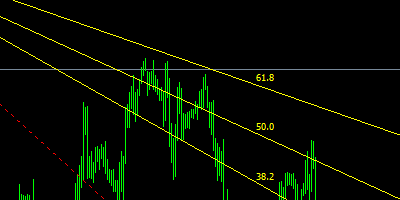
Fibonacci Arcs - half circles extending from the center of the circle outwards, connecting a high and a low, called the base line.
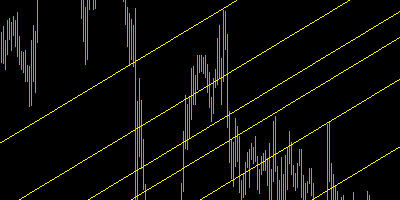
Fibonacci Channel - a variation of the fibonacci extension where the channels are plotted diagonally.
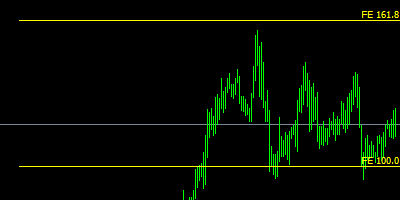
Fibonacci Expansion - expansions of the price, the opposite of retracement.
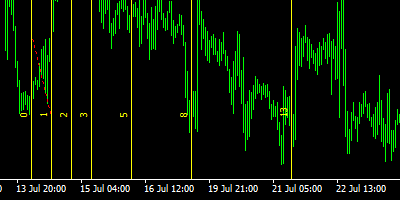
Fibonacci Time Zones - Fibonacci levels that are applied to time and predict levels based on time/date rather than price.
Jak korzystać z kalkulatora Fibonacciego?
Simply enter a high value, a low value and an optional custom value and click the calculate button - you will instantly receive 8 retirement values and 6 extension values which you can easily plug into your forex trading system.
Are the Fibonacci Retracements useful in day trading?
Fibonacci retracement tool can be used in any timeframe and any trading style whether it is short term trading (scalping) or long term (trend following). It is considered to be more meaningful in longer timeframes (ie 30 minutes and above) to reduce short term market noise.
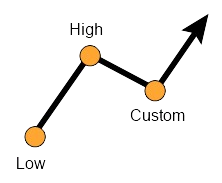
How to use Fibonacci retracement in an uptrend?
Using a low as a starting point and the high as the end point, the calculated retracements will act as support levels while the extensions will act as resistance levels.
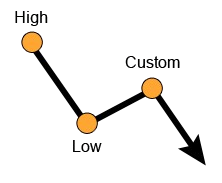
How to use Fibonacci retracement in a downtrend?
Using a high as a starting point and a low as the end point, the calculated retracements will act as resistance levels while the extensions will act as support levels.
[1] More on Leonardo Pisano Bigollo https://en.wikipedia.org/wiki/Fibonacci